体渲染-随笔

本篇是随笔, 虽然写了很久, 但是乱写

写了我好久, 感觉高数都还回去了.

寒假是真的无聊…在22: 27看高数的绝望…

引入

体渲染是一种渲染模型, 也可以认为是一种渲染思路. 在Mesh的渲染中, 我们认为场景其实是面片+材质, 而体渲染认为物体应当是个有体积的东西. 光穿过物体, 在这个过程中不断与物体发生作用, 最后得到结果.

体渲染的引入, 一开始是为了解决云, 烟雾这类物体的渲染. 可以认为, 面片渲染只考虑了光与物体表面的作用, 没有考虑光在物体内部的行为. 这在大部分物体上可能没有什么问题, 例如玻璃与金属, 几乎所有光学行为都发生在表面. 但是当问题复杂一些: 我想要体现水中的丁达尔效应, 我想要渲染逼真的云雾, 面片模型就难以胜任. 一种解决方法是将丁达尔效应建模成简单的射线, 再套用一个衰减函数. 但有时候云雾并不完全是这样的, 光也会在内部散射, 甚至粒子有自发光, 云雾并不均匀. 于是, 我们不如考虑光在场景中的整个行进过程, 而不是只考虑表面这种割裂情形. 这就是体渲染(Volume Rendering).

体渲染的计算

体渲染的基本计算方法就是体渲染积分, 最简单的Ray-casting方法, 思路是从摄像头向屏幕上每个像素生成一条射线, 沿射线积分辐射值, 得到最终的辐射值(RGB).

具体来说, 假如某个射线由一个参数$ t $来表达$ \bold{r}(t) $, $ \bold{r}(t) $是一个三维坐标. 射线方向用$ \bold{d} $表示, $ \bold{d} $是三维的笛卡尔单位向量, 或者是二维的球坐标向量. 物体实际上由两个函数表示, 第一个是辐射值函数$ \bold{C}(\bold{r}(t), \bold{d}) $, 值为一个辐射值(RGB), 表示体在$ \bold{r}(t) $处以$ \bold{d} $方向观察时的"发光"值, 用于累积最终辐射值. 例如一个被一束光穿过的云雾, 如果观察射线垂直于这束光, 则我们应该可以看到$ \bold{C} $在光束经过的附近的值为这束光的颜色. 我想表达的是, 在这个模型中, 场景中光源对体的影响, 已经考虑在$ \bold{C} $中了. 如果想要拆分出来, 需要从物理的手段, 对体渲染积分方程进行扩展. 第二个是密度函数$ \sigma(\bold{r}(t)) $, 其值为体在$ \bold{r}(t) $处的密度, 并且我们认为与观察方向无关. 密度的作用是计算光的遮挡: 你在$ \bold{r}(t) $处观察到的辐射, 会被视线上之前所有的体遮挡, 而密度就是各处的"遮挡强度", 甚至可以把$ \sigma(\bold{r}(t)) $理解成"单位长度削弱辐射值的比例". 例如, 我们可以认为不透明物体的内部密度非常大, 使得只有表面的辐射值能被累积到像素, 即表现成物体表面的颜色. 而透明物体的内部密度很小, 几乎不阻挡后面的辐射.

首先, 我们要计算$ \bold{r}(t) $之前一直到像素点的总留存率($ 1 - 总吸收率 $):

$$ \begin{align*} I代表&的是辐射值 \\ \bold{d}I &= -\sigma(\bold{r}(u)) I \bold{d}u \\ \frac{\bold{d}I}{I} &= -\sigma(\bold{r}(u))\bold{d}u \\ \int_{I_0}^{I_t}\frac{\bold{d}I}{I} &= -\int_0^t \sigma(\bold{r}(u))\bold{d}u \\ \ln{\frac{I_t}{I_0}} &= -\int_0^t \sigma(\bold{r}(u))\bold{d}u \\ 留存率 \ T(t) = \frac{I_t}{I_0} &= \exp(-\int_0^t \sigma(\bold{r}(u))\bold{d}u) \end{align*} $$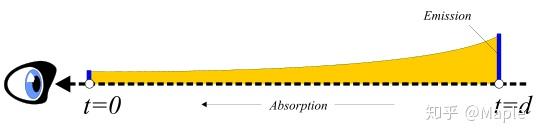

$ T(t) $也叫做光学深度.

那么, 像素的具体辐射值, 可以由射线路径上所有的辐射值乘以留存率积分得到:

$$ \int_0^{\infty} \bold{C}(\bold{r}(t), \bold{d}) \, T(t) \, \bold{d}t = \int_0^{\infty}\bold{C}(\bold{r}(t), \bold{d}) \exp(-\int_0^t \sigma(\bold{r}(u))\bold{d}u)\bold{d}t $$

积分离散化

计算机无法直接计算积分, 因此需要离散化. 一种常用的办法是将积分近似为级数.

首先第一步是把这个上限近似成一个大数. 虽然理论上来说要积分到无穷, 但是我们的场景一般也是有限的. 这里我们只积分到一个足够大的数$ M $.

$$ \int_0^{\infty} \bold{C}(\bold{r}(t), \bold{d}) \, T(t) \, \bold{d}t \approx \int_0^{M} \bold{C}(\bold{r}(t), \bold{d}) \, T(t) \, \bold{d}t $$

接着, 我们将区间$ [0, M] $拆分成$ n $个子区间$ [t_i, t_{i+1}] $, 并对这些区间分别积分:

$$ \int_0^{M} \bold{C}(\bold{r}(t), \bold{d}) \, T(t) \, \bold{d}t = \sum_{i=1}^n{\int_{t_i}^{t_{i+1}}\bold{C}(\bold{r}(t), \bold{d})T(t)\bold{d}t} $$

注意, 近似到黎曼和的过程中, 我们默认一个约定: 当$ n $足够大, $ \bold{C}(\bold{r}(t), \bold{d}) $与$ \sigma(\bold{r}(t)) $可以认为是保持不变的:

$$ \int_{t_i}^{t_{i+1}}\bold{C}(\bold{r}(t), \bold{d})T(t)\bold{d}t \approx \bold{C}_i \int_{t_i}^{t_{i+1}}T(t)\bold{d}t $$

这个式子中, 我们其实还需要计算$ \int_{t_i}^{t_{i+1}}T(t)\bold{d}t $, 将它用$ \sigma(\bold{r}(t)) $来表示, 来近似. 这个式子是个积分式, 而且积分里套积分, 看着很恐怖. 我们先看$ T(t) $:

$$ \begin{align*} T(t) &= \exp(-\int_0^t \sigma(\bold{r}(u))\bold{d}u) \\ &= \exp(-\int_0^{t_i} \sigma(\bold{r}(u))\bold{d}u - \int_{t_i}^{t} \sigma(\bold{r}(u))\bold{d}u) \\ &= \exp(-\int_0^{t_i} \sigma(\bold{r}(u))\bold{d}u) \cdot \exp(-\int_{t_i}^{t} \sigma(\bold{r} (u))\bold{d}u) \\ &= T(t_i) \cdot\exp(-\int_{t_i}^{t} \sigma(\bold{r} (u))\bold{d}u) \end{align*} $$

我们把它拆成两个部分, 分别是$ 0 \rightarrow t_i $与$ t_i \rightarrow t $.

接下来我们再看:

$$ \begin{align*} \int_{t_i}^{t_{i+1}}T(t)\bold{d}t &= \int_{t_i}^{t_{i+1}}T(t_i)\exp(-\int_{t_i}^t \sigma(\bold{r} (u))\bold{d}u)\bold{d}t \\ &= T(t_i) \int_{t_i}^{t_{i+1}}\exp(-\int_{t_i}^t \sigma(\bold{r} (u))\bold{d}u)\bold{d}t \\ &\approx T(t_i) \int_{t_i}^{t_{i+1}}\exp(-\sigma_i \cdot (t-t_i))\bold{d}t \\ &= T(t_i) (\left.\dfrac{\exp(-\sigma_i\cdot(t-t_i))}{-\sigma_i}\right|_{t_i}^{t_{i+1}}) \\ &= \frac{T(t_i)}{\sigma_i}(1-\exp(\sigma_i\cdot(t_{i+1}-t_i))) \end{align*} $$

至于$ T(t_i) $, 我们可以迭代式近似计算:

$$ \begin{align*} T(t_{i+1}) &= T(t_i) \cdot\exp(-\int_{t_i}^{t_{i+1}} \sigma(\bold{r} (u))\bold{d}u) \\ &\approx T(t_i) \exp(\sigma_i\cdot(t_i-t_{i+1})) \end{align*} $$

代入原式, 得:

$$ \begin{align*} \sum_{i=1}^n{\int_{t_i}^{t_{i+1}}\bold{C}(\bold{r}(t), \bold{d})T(t)\bold{d}t} &\approx \sum_{i=1}^n{(\bold{C}_i\int_{t_i}^{t_{i+1}}T(t)\bold{d}t)} \\ &= \sum_{i=1}^n{(\bold{C}_i\frac{T(t_i)}{\sigma_i}(1-\exp(\sigma_i\cdot(t_{i+1}-t_i))))} \end{align*} $$

最终得到:

$$ \int_0^{\infty} \bold{C}(\bold{r}(t), \bold{d}) \, T(t) \, \bold{d}t \approx \sum_{i=1}^n{(\bold{C}_i\frac{T(t_i)}{\sigma_i}(1-\exp(\sigma_i\cdot(t_{i+1}-t_i))))} $$

有关NeRF

我看到NeRF论文里似乎是多乘了个$ \sigma_i $:

$$ \int_0^{\infty} \sigma(\bold{r}(t)) \bold{C}(\bold{r}(t), \bold{d}) \, T(t) \, \bold{d}t $$

我的理解是, 辐射值与体密度也有关系, 密度越大, 发出的辐射值越大.

所以最终结果就会是:

$$ \int_0^{\infty} \bold{C}(\bold{r}(t), \bold{d}) \, T(t) \, \bold{d}t \approx \sum_{i=1}^n{(\bold{C}_iT(t_i)(1-\exp(\sigma_i\cdot(t_{i+1}-t_i))))} $$

把分母消去了, 看着更合理一些…