RoPE旋转位置编码学习笔记与代码实现

最近想写点torch，就打算手搓个llm预训练，于是就去拿llama3开刀。尝试去实现久闻大名的RoPE（旋转位置编码）的时候，搜到了这篇文章，然后就直接开看。奈何本人数学水平实在太差，横竖看不进去，总是不太能理解。于是就干脆对着公式写代码，经过一段痛苦的时间后，勉强挤出几十行代码，才算是对RoPE有了一些不严谨的理解。

最近心血来潮整的手搓llm结构与训练过程：SimpleLLM (应该会摆掉，应该…)

绝对位置编码的缺陷

绝对位置编码是这么做的：

是第m个位置的token进行词嵌入后得到的向量， 则是我们想要得到的，附加了位置信息的第m个位置的token对应的初始语义向量。原论文的绝对位置编码通过直接更改输入到模型内部的词嵌入向量的值，来实现附加位置信息。

这种方法非常符合直觉，在输入进模型之前进行某种意义上的“标号”，来附加位置信息。只要每个位置附加的信息都是独一无二的，那么它就可以作为这个位置的唯一标识。散落无章的一堆纸，只要有了页码，就可以排成一本书。

但是这个方法也有问题。至于是什么问题呢？本人对此有一些不成熟的思考：

我们先从llama3的训练中的一个细节出发：Attention is All You Need这篇论文中模型的训练，与BERT的训练，从它们的数据集中拿出某一个sample，那大概率是填不满上下文长度的，于是需要对上下文进行padding来达成固定长度。假设上下文长度为16K，甲sample的序列长度为1K，乙sample的序列长度为8K，两者都填充到了16K，开销上来看是差不多的，因为数据的规模一样大，都是一样计算（猜测可能内部有一些优化，但是不会差太多），但是从直觉上来说，应该是乙sample包含的有效信息更多，更加利于模型优化。

于是，很自然的，当模型上下文长度比较大，没多少sample能填满时，一个输入的序列应该由多个sample拼接而成，凑成一个比较接近上下文长度的序列，充分利用算力。当然了，为了防止某一个sample中的token进行注意力计算时，去查询了其它sample的token，mask也要进行一些改造。不过本篇文章的重点不是这个。

在这种情况下，我们其实希望位置编码的信息要有某种“等价性”：无论其中一个sample在哪个位置，位置编码信息应该不影响位置的表达。一个sample在拼接过程中被排在第一个，中间的位置，还是最后的位置，位置编码信息都应该具有某种共通的性质，因为这句话无论排在哪都是同一句话，位置编码出的向量都应该包含相同的信息。

这种特征的“空间平移不变性”，让人联想到CNN对于特征位置的不敏感。原因是CNN天生擅长捕捉像素相对位置的信息，毕竟本身结构的设计就是为了考虑相对位置。

所以要实现这种对于空间的绝对位置不敏感，无论在序列中的哪个位置都能表达相同的模式的编码方式，考虑相对位置信息很重要。

这么来看，原来的绝对位置编码的方式其实就有点不太合适了。为什么呢？我们观察一下原来绝对位置编码使用的Sinusoidal 函数：

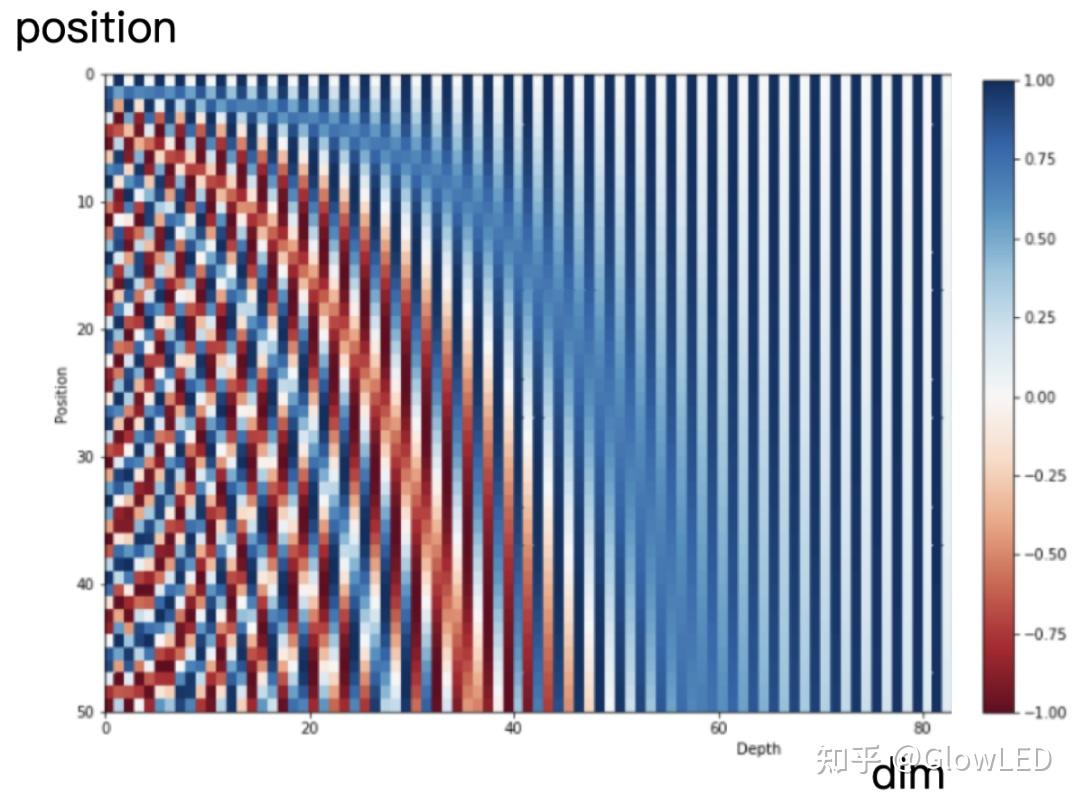
可以看到，Sinusoidal 函数基本不强调“相对位置信息”，不同的位置，甚至连变化的feature都不是同一个，例如，在position大约为0-5时，相邻位置编码信息在大于40的feature上几乎无变化。而当position增大后，feature较大的位置也发生了变化。位置之间的差距甚至都不是同一个feature，都不是一个方面的比较。

绝对位置编码错开了不同位置间差距的feature的位置，虽然充分利用了语义向量中的每个feature，但是也基本毁灭了相对位置信息的一致性。这使得同一个sample被拼接到开头，中间与结尾的位置信息都不太一样，模型需要花费额外的参数来去学习这种没有规律的不同。仿佛就是同样一句话只是因为开头被放在了不同位置，token之间的位置关系就变了。

现在我们放远视角，我们不仅关心llama3训练这种一输入多样本的情况。考虑大多数文章。同样一句话在文章的开头与结尾虽然有不同的绝对位置信息，但也应该具有相同的相对位置信息，而不是相对位置信息有很大差别。

为了解决这个问题，我们人为地设计一种可以在绝对位置信息的基础上表达相对位置信息的规律，这样模型能很容易地学习到这个规律。这就有了RoPE。而RoPE选择的规律是角度。

RoPE，旋转位置编码

与绝对位置编码不同，RoPE是在q，k，v生成之后，对q与k做手脚，来附加位置信息。附加完后，q，k再正常计算attn score，然后对v进行加权和（attention的正常流程）。

本人数学水平堪忧，中间过程怕讲错，所以这里直接看结果的几个式子：

上面这个式子就是我们想要的这样一个编码函数的表达式：它接受输入 (第m个token进行词嵌入后得到的向量)，以及位置m，输出编码后的向量 .这就是我们的目标，很简单纯粹。

右侧该函数的形式是 与两个矩阵相乘（分别是$W_{q,k}$与$R^d_{\Theta,m}$，这里W下标既有q又有k的意思其实是，当想编码的是q时，使用Wq，当想编码的是k时，使用Wk.

所以编码函数也能这么写：

其实就是把q与k分别乘以同一个编码矩阵 .

然后我们来看看这个编码矩阵：

看着有点复杂，但是我们先拿出来第一部分：

按照矩阵乘法的规则，它会作用这样一个向量（其它位置都是0，相当于不作用，不考虑）:

观察这个第一部分的编码矩阵 ,不难发现这其实是个旋转矩阵（以前学的图形学勉勉强强用上了点皮毛hhh），它右乘 的效果，就是将这个向量逆时针旋转$m\theta_0$.

那么扩展到整个编码矩阵 ，这个大矩阵的效果就是：将 （ 同理，这里就全部写q了）向量中的元素，按照$q_0$,$q_1$;$q_2$,$q_3$;…这样两两分组，每组元素组成的二维向量在平面上分别旋转$m\theta_0$;$m\theta_1$;…得到编码后的向量 .

你可能会说：哎呀哎呀，这转来转去的那么麻烦有啥用吗？说相对信息很重要，这也没看出来哪里有相对信息呀！

但是我们先来看这么一点：与绝对位置编码feature的变化没啥规律不同，RoPE中同一组的feature都是在同一个平面上进行旋转变换，不同的位置，无论你是m还是n，不过是差了整数倍 的旋转角度。

而第m个token与第n个token之间的位置差距，不过就是差了旋转（m-n）个 的差距。并且相同组的feature， 与旋转的平面都是相同的。这就将位置信息中的相对位置信息，编码进了”多少个 的旋转角度差距“。这在数字上看似乎是不太明显的规律。但是对于模型来说，通过训练，它可以较为容易地学习到这个规律。

代码实现

首先，编码矩阵 比较大，又很稀疏，同时也很有规律，所以可以尝试进行一些化简：

$\odot$（Hadamard product，哈达玛积）就是对应元素相乘，在torch中就是普通的*符号。

llama3中的实现就是这种方法，不过我的代码是这么实现的：

这里不是相邻元素分组，而是上半段元素与下半段元素分组。例如： 与 ， 与 , 与 .之所以可以这么做，是因为在进行分组之前，features之间并没有什么顺序，任意分组都不会有什么影响。这样上半段与下半段分别分组的方法，也是ChatGLM使用的方法。

代码：

import torch
from torch import nn

class RoPE(nn.Module):
    def __init__(self, d: int, max_n: int, base: float=10000.0) -> None:
        super().__init__()
        self.d = d
        self.max_n = max_n
        self.base = base
        
        # 先生成从\theta_0到\theta_{d/2-1}的全部\theta
        thetas = (base ** (-torch.arange(0, d, 2).float() / d)).unsqueeze(0)  # [1, d/2]
        
        # 拼接一下，形成从0到d/2-1，再从0到d/2-1的序列
        thetas = torch.cat([thetas, thetas], dim=1)  # [1, d]
        
        # 生成m\theta,这里利用了broadcast机制
        idx = torch.arange(1, max_n+1).float().unsqueeze(1)  # [max_n, 1]
        thetas = thetas * idx  # [max_n, d]
        
        # 计算一下sin与cos值
        cos_cached = torch.cos(thetas)  # [max_n, d]
        sin_cached = torch.sin(thetas)  # [max_n, d]
        
        # 注册一下变量
        self.register_buffer('cos_cached', cos_cached)  # [max_n, d]
        self.register_buffer('sin_cached', sin_cached)  # [msx_n, d]
        
        # 类型注释，可无
        self.cos_cached: torch.Tensor
        self.sin_cached: torch.Tensor
        
        
    def forward(self, x: torch.Tensor) -> torch.Tensor:
        '''
        Args:
            x: [batch_size, seq_len, d]
        Returns:
            o: [batch_size, seq_len, d]
        '''
       
        _, n, d = x.size()
        
        # 切片切出来需要的长度
        cos = self.cos_cached[:n, :].unsqueeze(0)  # [1, n, d]
        sin = self.sin_cached[:n, :].unsqueeze(0)  # [1, n, d]
        
        # 分别计算第一项和第二项，注意这里第二项进行了切片与拼接
        # 同时这里也利用了broadcast机制
        x_cos = x * cos
        x_sin = torch.cat([-x[:, :, d//2:], x[:, :, :d//2]], dim=-1) * sin

        o = x_cos + x_sin  # [batch_size, seq_len, d]
        
        return o

虽然看了不少资料，但是本人习惯比较差，难以考据都看了哪些资料，无法列举。

本篇文章中的想法与代码基本都是自己一个人弄的。本人见识浅薄，如果有问题或者是不同的意见，欢迎探讨。