强化学习基础-粗略过一遍

基本概念

场景描述

• Environment: 环境. 是一个外部系统, 智能体处于这个系统中，能够感知到这个系统并且能够基于感知到的状态做出一定的行动。

• state/observation: 状态/观测. 状态反映了世界的全部信息, 观测是状态的子集.

• agent: 智能体. 做出决策的个体.

• action: 动作. 不同的环境允许不同种类的动作，在给定的环境中，有效动作的集合经常被称为动作空间(action space)，包括离散动作空间(discrete action spaces)和连续动作空间(continuous action spaces).

• reward: 奖励. 是由环境给的一个标量的反馈信号(scalar feedback signal).

强化学习设想中, agent在environment中行动, 在某时刻获取observation, 采取action并促使environment做出改变. 在某些时刻可以获取reward. 强化学习的目标是使得reward总和最大化.

公理化

动作使用$ a $表示, 状态(观测)使用$ s $表示, 时刻使用$ t $表示.

1. Policy: 策略. 用于决定下一步做出什么行动.

   如果是确定性的, 一般用$ \mu $表示:

$$ a_t=\mu(s_t) $$

​ 如果是随机性的, 一般用$ \pi $表示:

$$ a_t \sim \pi(\cdot|s_t) $$

2. State Transition: 状态转移. 可以是确定的也可以是随机的. 一般认为是随机的. 可以用状态密度函数来表示:

$$ p(s'|s, a) = \mathbb{P}(S'=s'|S=s, A=a) $$

3. Return: 回报. 又称cumulated future reward, 一般表示为$ U $, 定义为:

   $$ U_t=R_t+R_{t+1}+R_{t+2}+R_{t+3}+\cdots $$

   其中$ R_t $为第$ t $时刻的奖励. $ U $即未来和当下所有奖励之和.

   有时候我们认为未来的奖励不如现在等值的奖励那么好, 所以我们会乘以一个discount rate $ \gamma $. $ \gamma \in (0, 1]$. $ U $被扩展为:

   $$ U=R_t + \gamma R_{t+1} + \gamma^2R_{t+2}+\gamma^3R_{t+3} + \cdots $$

4. Value Function: 价值函数.

   价值函数使用期望对未来的收益进行预测，一方面不必等待未来的收益实际发生就可以获知当前状态的好坏，另一方面通过期望汇总了未来各种可能的收益情况。使用价值函数可以很方便地评价不同策略的好坏。

5. State-value Function: 状态价值函数. 用于度量给定策略下, 某个状态的回报的期望. 用于评判状态的好坏.

6. Action-value Function: 行动价值函数. 用于度量给定策略和状态下, 采取某个行动的回报的期望. 用于评判动作的好坏.

算法分类

Model-Free 与 Model-Based

按照环境是否已知来划分的.

Model-Free就是不去学习与理解环境, 环境给出什么信息就是什么信息, 常见的方法有Policy Optimization和Q-learning.

Model-Based是去学习和理解环境，学会用一个模型来模拟环境，通过模拟的环境来得到反馈。Model-Based相当于比Model-Free多了模拟环境这个环节，通过模拟环境预判接下来会发生的所有情况，然后选择最佳的情况。

可以认为这里的Model指的是"对环境的建模".

On-Policy 与 Off-Policy

On-Policy指策略必须运行才能优化. 即策略必须在环境中做决策, 一边决策一边优化.

Off-Policy指策略是在场下优化的. 是先在环境中采样大量动作-状态-奖励序列, 然后再优化. 所以Off-Policy可以根据其它策略的序列进行优化.

Policy-Based 与 Value-Based

Policy-Based中, 动作从策略中采样得到. 即策略产生每个动作的概率, 然后agent采样这个概率分布, 获取当前应该执行的动作.

Value-Based中, 策略生成每个动作的价值. agent每次总是选择最高价值的动作.

这两者是可以结合的.

经典算法

Q-learning

在Q-learning中，我们维护一张Q-table，表的维数为：状态数S * 动作数A，表中每个数代表在当前状态S下可以采用动作A可以获得的未来收益的折现和。

例如:

状态\动作	action1	action2	action3	action4
state1	$ Q_{11} $	$ Q_{12} $	$ Q_{13} $	$ Q_{14} $
state2	$ Q_{21} $	$ Q_{22} $	$ Q_{23} $	$ Q_{24} $
state3	$ Q_{31} $	$ Q_{32} $	$ Q_{33} $	$ Q_{34} $

当我们的agent位于state1时, 它会选择四个动作中对应回报期望最大的那个行动. 这可以认为是行动价值函数.

Q函数就是这样一个行动价值函数. 它有两个输入: “状态"和"动作”.

$$ Q^{\pi}(s_t, a_t) = E[R_{t+1}+\gamma R_{t+2} +\gamma^2 R_{t+3} + \cdots | s_t, a_t] $$

我们可以把Q函数视为一个在Q-Table上滚动的读取器，用于寻找与当前状态关联的行以及与动作关联的列。它会从相匹配的单元格中返回 Q 值。这就是未来奖励的期望。

在我们探索之前, Q-table会被设置成一个设定值(通常是0). 在对环境的探索过程中, Q-table的值会通过Bellman方程迭代式更新, 以给出对$ Q(s, a) $越来越好的近似.

Deep Q Network (DQN)

Q-table的维护需要满足: 1. 动作与状态空间是离散的, 如果是连续的, 则需要想办法离散化. 2. 动作和状态空间最好别太大, 特别是面对无限的空间时, 需要想办法有限化.

就算是采用离散化和有限化, Q-table的维护依然很麻烦. 问题复杂时, 项数实在太多了.

这时候一个很显然的思路是使用一个参数化的函数来表示Q-table. 而神经网络就很符合要求.

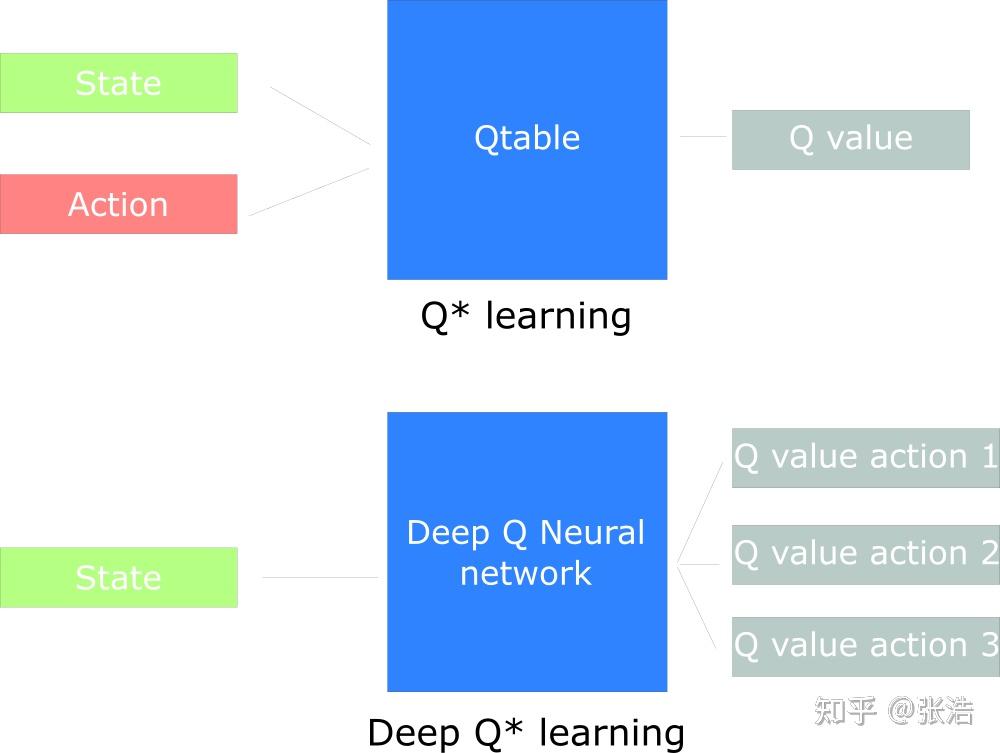
Q-table表示的Q函数, 需要提供state与action两项来检索. 而在DeepQLearning中, 我们用神经网络表示的Q函数只需要提供state, 返回的是所有action的Q值. 即返回原先Q-table中的一行.

这么做我想是因为神经网络最后一层输出不能太小. 如果像Q-table那样只输出一个值, 最后一层就太小了, 效率很低. 而且同时预测所有动作, 有利于网络更泛化地优化.

Q-learning与DQN都是off-policy的. 行为策略(如$ \epsilon $-greedy策略)与目标策略(用于评估和优化Q值的策略)是分离的. Q函数可以从过去任何策略产生的经验中学习(经验回放).

神经网络学习中, 一般来说, 目标是固定的. 而DQN中, Q是由Bellman方程计算得到, 是一个动态规划过程. 所以我们会让Q在一段实践内保持不变, 让神经网络更易于学习.

Policy Gradient

Q-learning与DQN都是基于价值的. 即学习的核心是对于动作价值的评估, 而根据价值采取行动则是简单的.

Policy Gradient是基于策略的. 大道至简, 输入状态, 输出为每个动作的概率, 即输出动作的分布, agent直接从分布中采样动作(或者直接采取概率最大的动作).

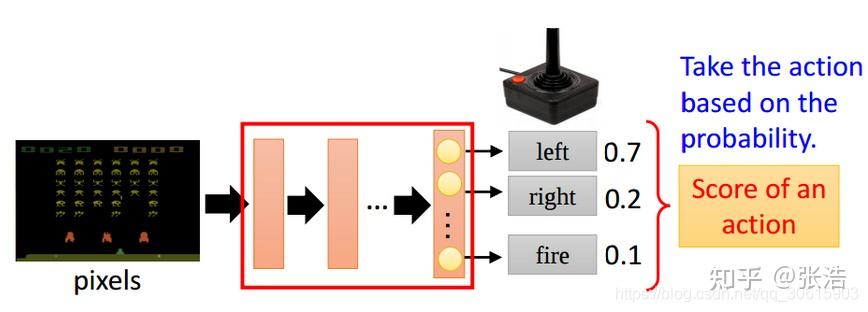
不过这样的话, 价值函数是隐式的, 比较难得到…

Actor Critic

Actor-Critic是Policy Based与Value Based的结合.

Actor指的是$ \pi_\theta (a | s) $, 即带参数$ \theta $的策略$ \pi $. Critic指的是值函数$ V^\pi(s) $, 对当前策略的值函数进行估计, 即评价策略的好坏. 即"在当前状态下, 采取策略$ \pi $, 我得到的回报的期望是多少?".

训练时, 同时训练这两个. 但其实我们最需要的是Actor. 所以本质上来说, Actor Critic算法是Policy Based的.